Understanding the Math Behind Gradient Descent Optimisation in Deep Learning

Introduction

Gradient descent is a fundamental optimisation algorithm widely used in training deep learning models. At its core, gradient descent seeks to minimise a given objective function, such as the error or loss function, by iteratively updating the model parameters. While mathematical equations often accompany explanations of gradient descent, this article aims to demystify the concept using an intuitive approach. Understanding this optimisation method is a crucial part of any comprehensive Data Science Course.

The Basics of Gradient Descent

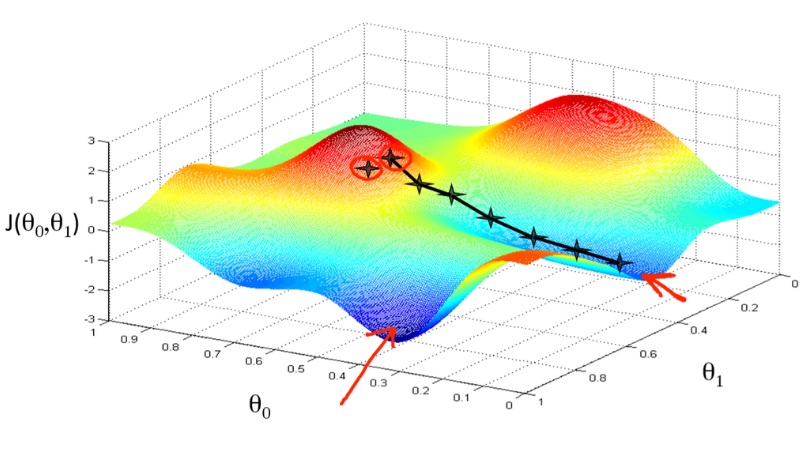
Imagine you are hiking in a mountainous region and your goal is to find the lowest point in the valley. You start at a random spot, look around, and decide to step downhill in the direction that seems steepest. With each step, you reassess your surroundings and adjust your direction to keep descending. This process continues until you can no longer go lower, indicating that you have likely reached the valley floor.

In the context of deep learning, the “mountain” represents the loss function—a measure of how far the model’s predictions are from the actual values. The “lowest point” is the minimum value of the loss function, where the model performs optimally. The steps you take downhill correspond to updating the model parameters, such as weights and biases. Learning these steps often forms the foundation of a career-oriented data course; for example, a Data Science Course in Mumbai tailored for professionals, as it is a key concept in building machine learning models.

How Gradient Descent Works

Gradient descent involves three key components:

Learning Rate: This determines the size of each step you take toward the minimum. A higher learning rate means larger steps, which can speed up the process but risks overshooting the minimum. A smaller learning rate ensures more precise steps but may take longer to converge.
Gradient: The gradient is a vector that points in the direction of the steepest ascent of the loss function. Since the goal is to minimise the loss, the algorithm moves in the opposite direction of the gradient.
Iterations: Gradient descent is an iterative process, meaning the algorithm updates the parameters repeatedly until the loss function reaches a satisfactory minimum or stops improving significantly. These iterative processes are frequently emphasised in a Data Science Course to help learners gain practical insights into model optimisation.

Types of Gradient Descent

Gradient descent comes in three main variants, each suited to different scenarios:

Batch Gradient Descent: In this approach, the algorithm calculates the gradient using the entire dataset in each iteration. While accurate, it can be computationally expensive and slow, especially for large datasets.
Stochastic Gradient Descent (SGD): Instead of using the whole dataset, SGD calculates the gradient for a single data point at each step. This makes it faster but introduces noise, causing the loss function to fluctuate rather than decrease smoothly.
Mini-Batch Gradient Descent: This strikes a balance between batch and stochastic gradient descent. It calculates the gradient using a small subset of data (mini-batch), combining the computational efficiency of SGD with the stability of batch gradient descent.

Challenges in Gradient Descent

Gradient descent is not without its challenges, and understanding these is crucial for effectively applying the algorithm:

Local Minima: The loss function may have multiple valleys (local minima). Gradient descent might get stuck in a local minimum rather than finding the global minimum.
Plateaus: Sometimes, the loss function has flat regions where the gradient is nearly zero. In these areas, progress can be exceedingly slow.
Saddle Points: These are points where the gradient is zero but the point is neither a maximum nor a minimum. The algorithm might waste time in these regions.
Vanishing and Exploding Gradients: In deep networks, gradients can become very small (vanishing) or very large (exploding), making it difficult to update parameters effectively.

Many of these challenges are explored in-depth in a Data Science Course, providing learners with tools and strategies to overcome them effectively.

Enhancements to Gradient Descent

To address its limitations, researchers have developed various modifications and optimisations to gradient descent:

Momentum: Momentum helps accelerate gradient descent in relevant directions and dampens oscillations. It does this by adding a fraction of the previous step to the current one.
Adaptive Learning Rates: Algorithms like AdaGrad, RMSProp, and Adam adjust the learning rate for each parameter individually based on past gradients. This adaptability helps handle challenges like vanishing gradients and speeds up convergence.
Gradient Clipping: To tackle exploding gradients, gradient clipping imposes a maximum threshold on gradient values.
Regularisation: Techniques like L1 or L2 regularisation add a penalty to the loss function, discouraging overly complex models and preventing overfitting.

Gradient Descent in Deep Learning

In deep learning, gradient descent is used to train neural networks by minimising the loss function. For example, in supervised learning, the loss function measures the difference between predicted outputs and actual labels. By applying gradient descent, the algorithm adjusts the network’s weights and biases to reduce this error over time.

Neural networks consist of layers of interconnected nodes, each with its own parameters. Backpropagation, a key technique in training neural networks, calculates the gradient of the loss function with respect to each parameter. This information is then used by gradient descent to update the parameters.

Practical Considerations

Successfully applying gradient descent requires careful tuning and experimentation:

Choosing the Learning Rate: An inappropriate learning rate can hinder convergence. Techniques like learning rate schedules or adaptive methods can help optimise this parameter.
Initialisation: The starting point of gradient descent can impact its performance. Poor initialisation might lead to slow convergence or getting stuck in undesirable regions.
Stopping Criteria: Deciding when to stop training is crucial. Common criteria include a predefined number of iterations, a threshold for loss improvement, or monitoring validation performance to prevent overfitting.

Conclusion

Gradient descent is the backbone of optimisation in deep learning, guiding models toward better performance by minimising the loss function. While the mathematical details can be intricate, the underlying intuition is simple and powerful. By understanding how gradient descent works, its challenges, and the techniques to enhance its effectiveness, practitioners can better harness this algorithm to train robust and efficient models. For anyone looking to master such concepts, enrolling in a professional-level data course in a premier learning centre, such as a Data Science Course in Mumbai, is an excellent starting point to build the necessary expertise.

Business Name: ExcelR- Data Science, Data Analytics, Business Analyst Course Training Mumbai
Address: Unit no. 302, 03rd Floor, Ashok Premises, Old Nagardas Rd, Nicolas Wadi Rd, Mogra Village, Gundavali Gaothan, Andheri E, Mumbai, Maharashtra 400069, Phone: 09108238354, Email: enquiry@excelr.com.